You probably know of Albert Einstein, the genius physicists with a bad haircut, shown in the picture above.  His famous relativity formula, e=mc², showed how much energy can be released from matter.  And it was related to the development of the first atomic bomb in the 1940′s.

By the way, the formula computes an astounding amount of energy from matter.  For example, I weigh 190 pounds.  Einstein’s formula says if the total nuclear forces of my body mass were released, it would be like exploding 1,860,000,000 tons of TNT.  That’s 88,403 times more explosive energy than the bomb that destroyed the city of Nagasaki, Japan in World War II… plus or minus a few kilotons.

Okay, so me exploding aside, what you may not know of is another one of Einstein’s formulas, t=72/r, called the Rule of 72.  It is one of the simplest rules to learn how to accumulate wealth.  And it shows how quickly you can double your money by compounding your investments in things like dividend paying stocks, interest paying accounts, etc.

Einstein called compounding and this formula the “eighth wonder of the world,” and the “greatest force on earth.”  That’s pretty powerful stuff coming from the guy whose formula is associated with the atomic bomb.

So let’s look at this greatest force on earth called compounding, because it’s key to your investing success.

Compounding is a way to increase your wealth with your investments.  And eventually double your money.  And then double it again… and again.  And we’ll talk about it in terms of you investing dividend paying stocks.  Because dividend stocks are easy to invest in, and one of the simplest ways to grow your wealth through compounding.

Okay, so I’m going to use some big numbers here at first, just to be a bit dramatic and help illustrate the point.  But we’ll get back to some real world numbers for you later.

So let’s say you invested $1,000,000 in a stock called My Big Stock (MBS) and it paid you a 10% dividend every year.  After your first year you’d have $1,100,000.  That’s your original $1,000,000 investment and a nice dividend payment of $100,000 ($1,000,000 X 10% = $100,000).

Hey, getting a $100,000 dividend check for one year is pretty nice, yes?

But instead of spending your $100,000 dividend, you invest it in even more MBS stock.

So now another year passes.  And at the end of Year 2, your $100,000 dividend from Year 1 gave you an additional $10,000 dividend ($100,000 X 10% = $10,000).  Geez, now you’re getting dividends on dividends.  That’s compounding!

Plus you also got another $100,000 in Year 2 on your original $1,000,000.

And you have the reinvested $100,000 dividend from Year 1.

So if you add it all up after Year 2, you’ve already grown your investment to $1,210,000 (your original $1,000,000, plus the Year 1 dividend of $100,000, plus the $10,000 dividend on that year 1 dividend in Year 2, plus you got another $100,000 on your original $1,000,000 in Year 2).

Okay, so it’s getting a little bit wordy to keep describing your compounding this way.  So here’s a table to show what happens in the next few years when you keep reinvesting your dividends (and their dividends on dividends) in MBS stock.

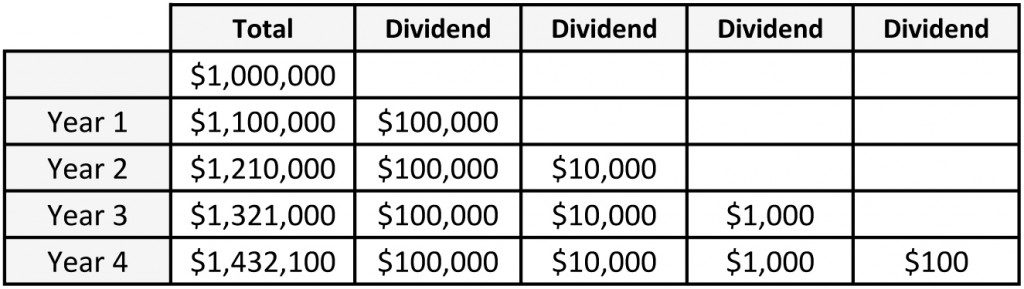
You can see that by Year 4 you are getting dividends ($100), on dividends ($1000), on dividends ($10,000), on dividends ($100,000).  Or put another way, you are making money, on money, on money, on money – that you never had to work for.

That’s compounding on steroids!

And you can see that if you keep doing this, at some point in the future you are going to double your money.

Doubling your money has a nice ring to it, doesn’t it?

So how many years will it take to double your money in this situation?  That’s the question Einstein asked, and solved, with his other equation of t=72/r.

And it’s drop dead simple to calculate.  All you do is take the percent you are getting in dividends (called the yield percent) and divide it into 72.

Since we said we were getting 10% in this example, then we will double our money in 10.2 years (72 / 10 = 10.2).   That’s all you need to know to figure it out!

For those interested in how the formula t=72/r says that, t is the time to double your investment in years, 72 is, well… 72, and r is the rate of return (or interest percent, or dividend percent, or dividend yield percent, same thing).

Anyhow, the formula has a number of uses.  For example, many readers have a 401k at work.  And when they go to their account web page it will show something like “Your year to date rate of return is 6.23%.”

So how long will it take for your 401k to double at that rate of return?  It will take 11.6 years (72 / 6.23 = 11.6).  Note that doesn’t take into consideration future contributions.

Or how about your savings account with the measly interest the banks pay.  As I write this, some of the top banks in the US only pay an interest rate of .01% on savings accounts.

So how long will it take to double your money in your savings account? It will take 7200 years (72 / .01 = 7,200).  So clearly the road to wealth is not in investing in savings accounts like this.

Or here’s one last example.  One of the best dividend stocks I ever invested in during the 2008 financial crisis was a company called MarkWest Energy.  At the time it was paying an astounding 20% dividend because the stock price had dropped so dramatically.  So how long would it take to double my money with that dividend?  Just 3.6 years (72 / 20 = 3.6).  And actually, I tripled my investment in less time because the stock price went back up too.

That’s how you build wealth.

You make sure that you have compounding going on in your investments.  And it’s why I’m so big on dividend paying stocks.  Because the dividends compound your investment over time.

Now the MarkWest Energy stock I mentioned was an exceptional situation due to the financial crisis.  So how about today, right now?

Well, everyone’s financial situation is different, so I can’t give individual advice.  But here’ a stock I’m invested in that pays a nice dividend.  It’s the communications company AT&T (T).  The stock symbol is T if you want to look it up on Yahoo https://finance.yahoo.com/quote/T?p=T.

As of this writing, it’s selling for $38.07 a share and has a dividend of 5.11%.  That’s a pretty nice dividend.  And AT&T increases their dividend by about 6% a year, so that’s even better.

So if you bought $1000 of AT&T stock, at a 5.11% dividend, and the stock price didn’t change, how long would it take for your investment to double using the Rule of 72?

It would take 14 years (72/5.11).  That’s actually pretty good, considering the stock price could rise over time, and especially if AT&T continues to increase their dividend by 6% a year.  So you would double your money even faster.

And it sure beats the 7200 years from some bank’s savings accounts.

And we know how to figure all of this out due to Einstein’s other formula, called the Rule of 72.

One final note, and that is that his rule of 72 is just a rule of thumb – it’s not exactly accurate, but pretty close.  And simple to use, too.  Because the exact formula to calculate how long to double your investment is something like this…

t=In(2)/(In(1+r/100))

Hey – who needs that?  It would take a genius to figure that out.  Fortunately, Einstein figured it out for us.  And his real genius is in the simplicity of his Rule of 72.

Remember, just divide 72 by the dividend or interest percent.

That’s all you need to do.

To your health and prosperity – John

P.S. To learn more about dividend stock investing, and how these dividends can compound and turn into your future paychecks, you can preview my latest book Your Future Paychecks And Raises: Get Dividend Checks In Your Mailbox Paid To The Order of You! right here for free.

P.P.S.  I think Einstein fudged the numbers a bit with his Rule of 72.  To learn about this little tidbit of history and more, read on…

What’s So Special About The Number 72 (I Think Einstein Fudged The Numbers)

So Einstein provided us with a simple tool to see how compounding, the greatest power on earth, could help us grow our wealth.

But how did he figure the formula out?  And what’s so magic about the number 72?

Well, I think he did something like this.  He asked the question, how long would it take to double my money at a 1% return?  Then he calculated it year by year.  And it took 72 years (hence the Rule of 72).

Why 1%?  Because it’s easy to calculate with (actually, some research says he used 10%, also an easy number to calculate with – but let’s go with 1%).  And we’re going to be like Einstein and figure out this rule too.

So let’s say we invest $1000 in a stock that pays a 1% dividend.  1% of $1000 is $10.  So after the first year we have $1010.

Let’s make this even easier.  Instead of calculating with 1% and then adding the $10 dividend to the original $1000, le’st just multiply by 1.01%.  That does the same thing.

So $1000 X 1.01 =  $1010.  That’s what you have for the first year.

Just do this 72 times on your calculator and your $1000 will double to $2000.

Or, you can just look at my calculations below – much easier.  And just skip to the bottom where it gets interesting.

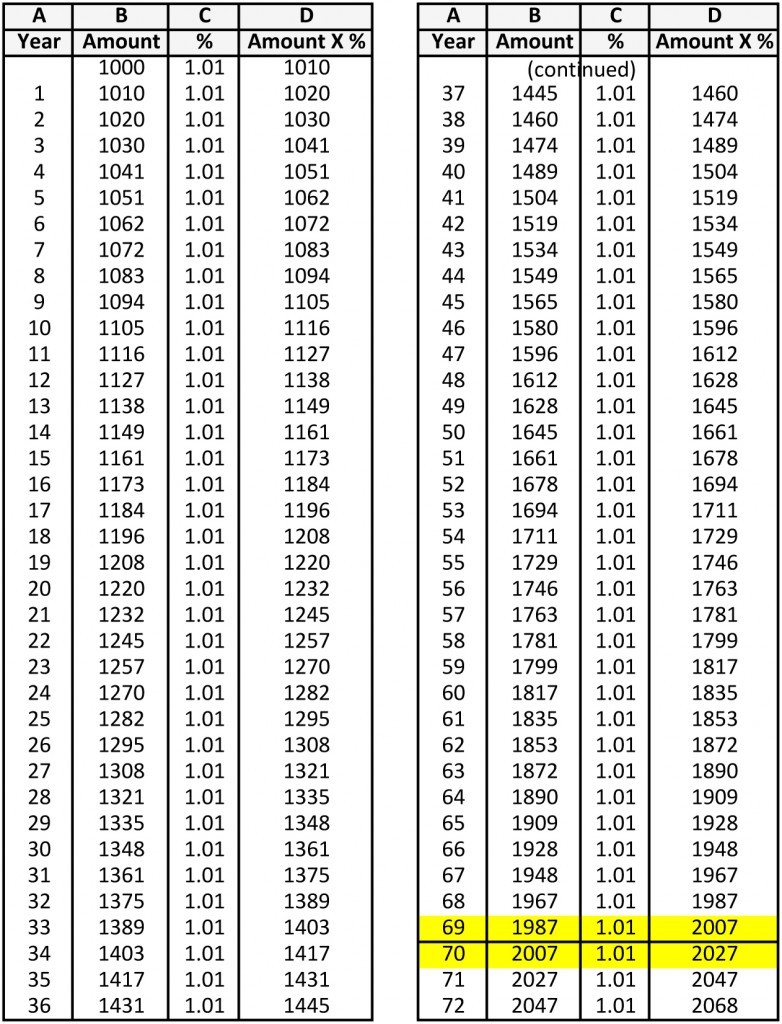
So then, scanning down my calculations, at year 72, the amount is now $2000.

Oops!  No, it’s not!  Houston, we’ve got a problem!  It’s more than $2000, it’s 2047!  In fact, we can see our money doubled to $2000 somewhere after year 69 but before year 70.

In fact, to be precise about it, I happen to know that it doubled in 69.3 years.

So what’s the deal?

Well, I think Einstein calculated all of this, came up with 69.3 years, and then he scratched his head, threw down his pencil and said,  “Ugggghhhh… Aber niemand wird sich an die Regel von 69.3 erinnern!”

Which roughly translated means, “Ugggghhhh… But nobody will remember the rule of 69.3!” (for our German readers, if that isn’t what it means, blame Google Translate .

Then he thought, “Hmmmm… maybe I’ll fudge the numbers a little bit and use 70… Nein, Nein (No, No), 70 is not divisible by very many numbers (because ALL mathematicians just love numbers that are divisible by other numbers for some reason).”

And then he thought, “Ugggghhhh, 71 is even worse, it’s a prime number not divisible by anything but 1 and itself.”

And then he thought, “Ahhhhhh, 72, now that there is a gute (good) number… easy to remember, and divisible by all kinds of numbers like 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72.”

So he fudged the math a bit and used the number 72 rather than 69.3, because, hey, this was just supposed to be an easy (approximate) rule of thumb.  And if we say it takes 72 years to double at 1%, then it’s just easier to work out many other percents in whole numbers, like it takes 36 years at 2%, or 18 years at 4%, or 9 years at 8%, etc.

Okay, so I may have made some of that stuff up.  Especially the part about ALL mathematicians loving numbers divisible by other numbers.  But in fact, I do believe Einstein fudged the math, and just went with 72 for an easy to remember Rule of 72.  And some research actually suggests this.

And aren’t we glad he did.

Because all we have to do is remember to divide 72 by the rate of return to find out “approximately” how quickly we can double our investment.

The genius of the rule is in its simplicity.

Compounding On Steroids

So while we’re talking about compounding and atomic bombs, I thought about the nuclear reaction that Einstein’s e=mc² formula related to.

The nuclear reaction in an atomic bomb works off of the compounding principle also, and illustrates it quite well.  As you can see in the image below, the first atomic bomb used uranium for the reaction.  And when a neutron hits the first uranium atom, it splits it, releasing energy and more neutrons.

Then these neutrons hit many more atoms, releasing even more energy, and even more neutrons.  And you have this rapidly compounding reaction of more and more neutrons, hitting more and more atoms, and releasing more and more energy – until the whole thing explodes.

And this atom splitting process compounds so rapidly that this all happens in an instant.  Flash!  Boom!

That’s compounding on steroids!

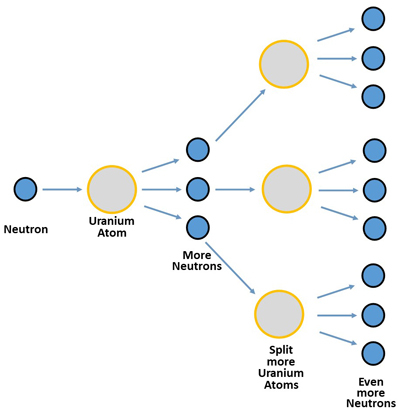
And looking at the chain reaction above, it’s tempting to wonder if Einstein thought about this nuclear compounding as well.

But he may not have – at least not at first, according to this surprising tidbit of history for you.

You see, during World War II, there was great concern among physicists that Germany might develop the atomic bomb.  So because of this concern, two physicists in particular, Leo Szilárd and Eugene Wigner, drove in Wigner’s car to Einstein’s home in Long Island, New York.  They wanted him to send a letter to President Roosevelt to warn him.

When they explained to him the possibility of this compounding chain reaction and atomic bombs, Einstein, that genius creator of the formula e=mc², said, “Daran habe ich gar nicht gedacht (I did not even think about that).”

Interesting, isn’t it?  He must have been so deep into his theory of relativity that this had not occurred to him.

In any event, the letter was eventually written, Einstein signed it and it was sent to President Roosevelt.  And that caused the creation of the Manhattan Project, where the US began the race to develop the first atomic bomb.

Which lead to the extreme compounding effect of nuclear reactions, dramatically demonstrated at 5:29 a.m. on July 16, 1945, with the detonation of the first test bomb in Alamogordo, New Mexico.

And the rest is history.

Okay, so historical tidbits aside, and to wrap things up, here’s our final rule of thumb.

When it comes to compounding, you don’t want to be anywhere near it if it involves uranium.

But as Einstein said, “Compounding is the greatest force on earth.”  So you definitely want it to happen with your investments.

So just remember, if you want to know how many years your investment will take to compound and double, just divide 72 by the rate of return (or dividend yield, or interest rate).

And that’s probably all you ever wanted to know about Einstein’s Rule of 72.

Enough said.

You can do this!